Please have a look at 👉🏻question👈🏻 first.

Key observations

There are some important key observations in the problem statement

• Two consecutive words can only determine lexicographic relationship between two characters based on the common prefix. Example: dcab followed by dcak specifies that k comes after b lexicographically within the alien dictionary, dca being the common prefix
• There can be more than one possible correct lexicographic orderings
• Letters within the word don't determine any ordering amongst themselves (lexicographical relationships only specify the relative ordering amongst the words)

First observation is important since it helps establish relationships between individual characters.

Algorithm

The relationships between characters can simply be created by using graphs. Reason will become clear from the graph within the example👇🏻. The characters become nodes within the graph. The relationships we extract from the ordering of words becomes our edges.

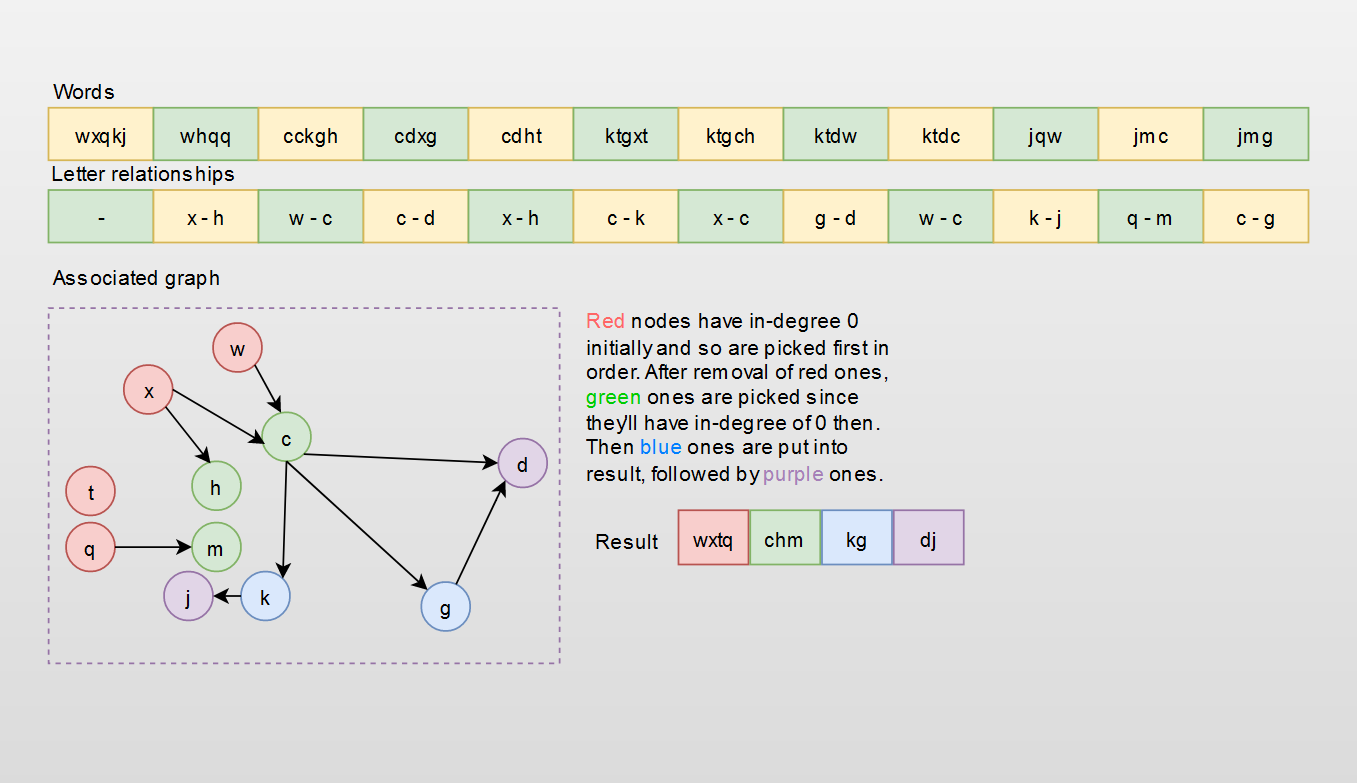
After our graph is ready, we just need to establish the topologically sorted order. And for that, we can use in-degree of our graph nodes(Kahn's algorithm) if we are using BFS. DFS can be used as well but we'll need to reverse our result.

Two edge cases(found out the hard way)

• A prefix can exist in the input list after the word(cab after cabua), but will result in invalid ordering
• Lexographic output must contain all unique letters that were within the input list. If not, the order can't exist.

java
public class Solution {
	public String alienOrder(String[] words) {
		Set<Character> set = new HashSet<>();
		StringBuilder sb = new StringBuilder("");
			if(words.length==1){
				for(char c: words[0].toCharArray()) if(!set.contains(c)){
					set.add(c); sb.append(c);
				}
				return sb.toString();
			}
		boolean [][]adjMatrix = new boolean[26][26];
		int []indegree = new int[26];
		Arrays.fill(indegree, -1); //in-degree -1 means node doesn't exist
		for(int i=1; i<words.length; i++){
			char[] word1 = words[i-1].toCharArray();
			char[] word2 = words[i].toCharArray();
			for(int j=0; j<word1.length; j++){
				if(indegree[word1[j]-'a'] == -1 ) { indegree[word1[j] - 'a'] = 0; set.add(word1[j]); }
			}
			for(int j=0; j<word2.length; j++){
				if(indegree[word2[j]-'a'] == -1 ) { indegree[word2[j] - 'a'] = 0; set.add(word2[j]); }
			}
       int j=0;
			for(; j<word1.length&&j<word2.length; j++){
				if(word1[j] != word2[j]){
					if(!adjMatrix[word1[j]-'a'][word2[j]-'a']){//build adjacency-list and in-degree map
						adjMatrix[word1[j]-'a'][word2[j]-'a'] = true;
						indegree[word2[j]-'a']++;
					}
					break;
				}
                
			}
			if(j==word2.length && word1.length>word2.length){//edge case 1
				return "";
			}
		}
		while(true){
			boolean isV = false;
			for(int i=0; i<indegree.length; i++){
				if(indegree[i]==0) {//select nodes with in-degree 0 and add to result
					sb.append((char)('a'+i));
					indegree[i] = -1;
					set.remove((char)('a'+i));
					for(int j=0; j<26; j++){
						if(adjMatrix[i][j]) indegree[j]--;//reduce the in-degree's of all dependent nodes
					}
					isV = true;
				}
			}
			if(!isV) break;
		}
		return set.isEmpty()? sb.toString(): "";//edge case 2
	}
}

Points to note

In my implementation I have used Adjacency-matrix and not the Adjacency-list, because of question constraints. For storing in-degree's I have used a simple primitive array, 'coz of the same reason. Had the constraints needed more scale I would have used HashMap based implementation for maintaining Adjacency-list and in-degree's

One last thing about above piece of code, I haven't exactly used BFS, since in-degree map itself can be used to mimic the operations of BFS in topological sorting. However at scale above approach will be very expensive due to repetitive usage of for(...) loop. In that case we must use Queue for mimicking BFS operations.

DFS code

Simple DFS can return topological sort but in reversed order. The tricky part is to detect cycles and for that instead of using a simple boolean visited array, we must use int array having three possible values

• 0 for unvisited nodes
• -1 for visited but not fully processed nodes
• 1 for visited and fully processed nodes

If during our DFS we find any node with visited value as -1 we can say for sure we have a cycle and hence we return false.

java
public class Solution {
	boolean [][]adjMatrix;
	StringBuilder sb;
	Set<Character> set;
	int visited[];
	public String alienOrder(String[] words) {
		set = new HashSet<>();
		sb = new StringBuilder("");
		if(words.length==1){
			for(char c: words[0].toCharArray()) if(!set.contains(c)){
				set.add(c); sb.append(c);
			}
			return sb.toString();
		}
		adjMatrix = new boolean[26][26];
		for(int i=1; i<words.length; i++){
			char[] word1 = words[i-1].toCharArray();
			char[] word2 = words[i].toCharArray();
			for(char ch: word1) set.add(ch);
			for(char ch: word2) set.add(ch);
      int j=0;
			for(; j<word1.length&&j<word2.length; j++){
				if(word1[j] != word2[j]){
					if(!adjMatrix[word1[j]-'a'][word2[j]-'a']){ // flip these two indexes to get a reverse-adjacency-matrix
						adjMatrix[word1[j]-'a'][word2[j]-'a'] = true;
					}
					break;
				}
			}
			if(j==word2.length && word1.length>word2.length){ // prefix after string check
				return "";
			}
		}
		visited = new int[26];
		for(int i=0; i<visited.length; i++){
			if(set.contains((char)('a'+i)) && !DFS((char)('a'+i)) ) return "";
		}
		return set.isEmpty()? sb.reverse().toString(): "";
	}
    
	private boolean DFS(char curr){
		if(visited[curr-'a'] == -1){ // cycle found
			return false;
		}
		if(visited[curr-'a'] == 1){ // already visited node
			return true;
		}
		visited[curr-'a'] = -1;
		for(int i=0; i<adjMatrix.length; i++){
			if(set.contains((char)('a'+i)) && adjMatrix[curr-'a'][i] && !DFS((char)('a'+i)) ) {
				return false;
			}
		}
		visited[curr-'a'] = 1;
		set.remove(curr);
		sb.append(curr);
		return true;
	}
}

Now, instead of using a adjacency matrix we could also have used reverse adjacency matrix(or list) if we'd don't want to reverse our resulting string.

Complexity computational complexity

There are three parts within the algorithm and so our calculations become,

T(N,C,U) = O(2*C) # computing relationships bw. characters
            + O(U) + O(min(U^2, N-1)) # building the graph
            + O(U+min(U^2, N-1)) # topological sorting
         = O(C+U+min(U^2, N))
         = O(C+min(U^2, N)) # C >= U
         = O(C+N) = O(C) # U^2 >= N since U^2 was meant to act as an upper bound for N

U is total number of unique characters, N is number of words and C is sum of length of all words within the dictionary. Initially I used the the maximum word length as C in my calculations but I got stuck with the min(...). So, had to use C this way to reach a conclusive formulation.

Important thing to note here is that we can have atmost U^2 nodes in the graph and if we have a lot of words and hence a lot of relationship edges it becomes an upperbound for N-1.

Similarly for memory complexity,

T(N,C,U) = O(U) # visited set
         + O(min(U^2, N-1)) # adjacency matrix or list
         = O(U+min(U^2, N))

Hopefully you got it. By the way, if you already have found, or do find a better solution, do enlighten🌅 me.

Cheers guys, be awesome ⛄.

P.S. Thanks Alienware for the cute image and for the best laptops I played my games in....